find两个给定节点之间的path?
假设我有以下方式连接的节点,我如何到达给定点之间存在的path数目以及path细节?
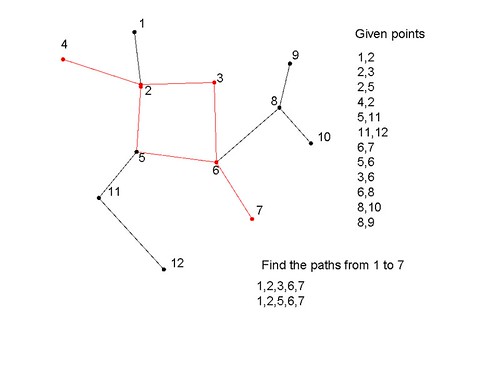
1,2 //node 1 and 2 are connected 2,3 2,5 4,2 5,11 11,12 6,7 5,6 3,6 6,8 8,10 8,9 find从1到7的path:
答:find2条path
1,2,3,6,7 1,2,5,6,7
在这里find的实现很好,我将使用相同的
这里是上面的链接在Python中的片段
# a sample graph graph = {'A': ['B', 'C','E'], 'B': ['A','C', 'D'], 'C': ['D'], 'D': ['C'], 'E': ['F','D'], 'F': ['C']} class MyQUEUE: # just an implementation of a queue def __init__(self): self.holder = [] def enqueue(self,val): self.holder.append(val) def dequeue(self): val = None try: val = self.holder[0] if len(self.holder) == 1: self.holder = [] else: self.holder = self.holder[1:] except: pass return val def IsEmpty(self): result = False if len(self.holder) == 0: result = True return result path_queue = MyQUEUE() # now we make a queue def BFS(graph,start,end,q): temp_path = [start] q.enqueue(temp_path) while q.IsEmpty() == False: tmp_path = q.dequeue() last_node = tmp_path[len(tmp_path)-1] print tmp_path if last_node == end: print "VALID_PATH : ",tmp_path for link_node in graph[last_node]: if link_node not in tmp_path: #new_path = [] new_path = tmp_path + [link_node] q.enqueue(new_path) BFS(graph,"A","D",path_queue) -------------results------------------- ['A'] ['A', 'B'] ['A', 'C'] ['A', 'E'] ['A', 'B', 'C'] ['A', 'B', 'D'] VALID_PATH : ['A', 'B', 'D'] ['A', 'C', 'D'] VALID_PATH : ['A', 'C', 'D'] ['A', 'E', 'F'] ['A', 'E', 'D'] VALID_PATH : ['A', 'E', 'D'] ['A', 'B', 'C', 'D'] VALID_PATH : ['A', 'B', 'C', 'D'] ['A', 'E', 'F', 'C'] ['A', 'E', 'F', 'C', 'D'] VALID_PATH : ['A', 'E', 'F', 'C', 'D']
广度优先search遍历一个图,并且实际上从一个起始节点查找所有path。 通常情况下,BFS并不保留所有path。 相反,它会更新一个前置函数π来保存最短path。 您可以轻松地修改algorithm,使π(n)不仅存储一个前驱,而且还存储一个可能的前驱列表。
然后在这个函数中编码所有可能的path,并且recursion遍历π得到所有可能的path组合。
在Cormen 等人的“ algorithm导论”(Introduction to Algorithms)中可以find使用这种符号的好的伪代码。 并随后在许多大学的脚本中使用这个主题。 谷歌search“BFS伪码前辈π” 在Stack Exchange上击中了这个命中 。
对于那些不是PYTHON专家的人,在C ++中是相同的代码
//@Author :Ritesh Kumar Gupta #include <stdio.h> #include <vector> #include <algorithm> #include <vector> #include <queue> #include <iostream> using namespace std; vector<vector<int> >GRAPH(100); inline void print_path(vector<int>path) { cout<<"[ "; for(int i=0;i<path.size();++i) { cout<<path[i]<<" "; } cout<<"]"<<endl; } bool isadjacency_node_not_present_in_current_path(int node,vector<int>path) { for(int i=0;i<path.size();++i) { if(path[i]==node) return false; } return true; } int findpaths(int source ,int target ,int totalnode,int totaledge ) { vector<int>path; path.push_back(source); queue<vector<int> >q; q.push(path); while(!q.empty()) { path=q.front(); q.pop(); int last_nodeof_path=path[path.size()-1]; if(last_nodeof_path==target) { cout<<"The Required path is:: "; print_path(path); } else { print_path(path); } for(int i=0;i<GRAPH[last_nodeof_path].size();++i) { if(isadjacency_node_not_present_in_current_path(GRAPH[last_nodeof_path][i],path)) { vector<int>new_path(path.begin(),path.end()); new_path.push_back(GRAPH[last_nodeof_path][i]); q.push(new_path); } } } return 1; } int main() { //freopen("out.txt","w",stdout); int T,N,M,u,v,source,target; scanf("%d",&T); while(T--) { printf("Enter Total Nodes & Total Edges\n"); scanf("%d%d",&N,&M); for(int i=1;i<=M;++i) { scanf("%d%d",&u,&v); GRAPH[u].push_back(v); } printf("(Source, target)\n"); scanf("%d%d",&source,&target); findpaths(source,target,N,M); } //system("pause"); return 0; } /* Input:: 1 6 11 1 2 1 3 1 5 2 1 2 3 2 4 3 4 4 3 5 6 5 4 6 3 1 4 output: [ 1 ] [ 1 2 ] [ 1 3 ] [ 1 5 ] [ 1 2 3 ] The Required path is:: [ 1 2 4 ] The Required path is:: [ 1 3 4 ] [ 1 5 6 ] The Required path is:: [ 1 5 4 ] The Required path is:: [ 1 2 3 4 ] [ 1 2 4 3 ] [ 1 5 6 3 ] [ 1 5 4 3 ] The Required path is:: [ 1 5 6 3 4 ] */
Dijkstra的algorithm更适用于加权path,这听起来像海报想要find所有path,而不仅仅是最短path。
对于这个应用程序,我会build立一个图表(你的应用程序听起来像不需要定向),并使用你最喜欢的search方法。 这听起来像是你想要所有的path,而不是对最短path的猜测,所以使用你select的一个简单的recursionalgorithm。
唯一的问题是如果graphics可以是循环的。
随着连接:
- 1,2
- 1,3
- 2,3
- 2,4
在寻找1-> 4的path时,可以有1→2→3→1的循环。
在这种情况下,我会保持堆栈遍历节点。 这是一个列表,包含该图表的步骤以及生成的堆栈(对于格式化 – 无表选项):
当前节点 (可能的下一个节点减去我们来自哪里)[stack]
- 1 (2,3)[1]
- 2 (3,4)[1,2]
- 3 (1)[1,2,3]
- 1 (2,3)[1,2,3,1] //错误 – 堆栈中的重复号码 – 检测到周期
- 3 ()[1,2,3] //回退到节点3并从堆栈中popup1。 没有更多的节点从这里探索
- 2 (4)[1,2] //后退到节点2并从堆栈中popup1。
- 4 ()[1,2,4] //find目标节点 – 为pathlogging堆栈。 没有更多的节点从这里探索
- 2 ()[1,2] //后退到节点2,popup堆栈4。 没有更多的节点从这里探索
- 1 (3)[1] //后退到节点1,popup堆栈2。
- 3 (2)[1,3]
- 2 (1,4)[1,3,2]
- 1 (2,3)[1,3,2,1] //错误 – 堆栈中的重复号 – 检测到周期
- 2 (4)[1,3,2] //后退到节点2并从堆栈中popup1
- 4 ()[1,3,2,4]find目标节点 – loggingpath的堆栈。 没有更多的节点从这里探索
- 2 ()[1,3,2] //后退到节点2并从堆栈中popup4。 没有更多的节点
- 3 ()[1,3] //后退到节点3,popup堆栈2。 没有更多的节点
- 1 ()[1] //后退到节点1并从堆栈中popup3。 没有更多的节点
- 用2个loggingpath[1,2,4]和[1,3,2,4]
原始代码有点麻烦,如果您想使用BFS来查找图表上2个点之间是否存在path,您可能需要使用collections.deque。 这是一个快速解决scheme,我砍了:
注意:如果两个节点之间不存在path,则此方法可能会无限地继续。 我没有testing过所有的情况,YMMV。
from collections import deque # a sample graph graph = {'A': ['B', 'C','E'], 'B': ['A','C', 'D'], 'C': ['D'], 'D': ['C'], 'E': ['F','D'], 'F': ['C']} def BFS(start, end): """ Method to determine if a pair of vertices are connected using BFS Args: start, end: vertices for the traversal. Returns: [start, v1, v2, ... end] """ path = [] q = deque() q.append(start) while len(q): tmp_vertex = q.popleft() if tmp_vertex not in path: path.append(tmp_vertex) if tmp_vertex == end: return path for vertex in graph[tmp_vertex]: if vertex not in path: q.append(vertex)
在Prolog(特别是SWI-Prolog)
:- use_module(library(tabling)). % path(+Graph,?Source,?Target,?Path) :- table path/4. path(_,N,N,[N]). path(G,S,T,[S|Path]) :- dif(S,T), member(SI, G), % directed graph path(G,I,T,Path).
testing:
paths :- Graph = [ 1- 2 % node 1 and 2 are connected , 2- 3 , 2- 5 , 4- 2 , 5-11 ,11-12 , 6- 7 , 5- 6 , 3- 6 , 6- 8 , 8-10 , 8- 9 ], findall(Path, path(Graph,1,7,Path), Paths), maplist(writeln, Paths). ?- paths. [1,2,3,6,7] [1,2,5,6,7] true.
给定邻接matrix:
{0,1,3,4,0,0}
{0,0,2,1,2,0}
{0,1,0,3,0,0}
{0,1,1,0,0,1}
{0,0,0,0,0,6}
{0,1,0,1,0,0}
下面的Wolfram Mathematica代码解决了这个问题,find了图中两个节点之间的所有简单path。 我使用简单的recursion和两个全局variables来跟踪周期和存储所需的输出。 为了代码清晰起见,代码还没有被优化。 “印刷品”应该有助于澄清它是如何工作的。
cycleQ[l_]:=If[Length[DeleteDuplicates[l]] == Length[l], False, True]; getNode[matrix_, node_]:=Complement[Range[Length[matrix]],Flatten[Position[matrix[[node]], 0]]]; builtTree[node_, matrix_]:=Block[{nodes, posAndNodes, root, pos}, If[{node} != {} && node != endNode , root = node; nodes = getNode[matrix, node]; (*Print["root:",root,"---nodes:",nodes];*) AppendTo[lcycle, Flatten[{root, nodes}]]; If[cycleQ[lcycle] == True, lcycle = Most[lcycle]; appendToTree[root, nodes];, Print["paths: ", tree, "\n", "root:", root, "---nodes:",nodes]; appendToTree[root, nodes]; ]; ]; appendToTree[root_, nodes_] := Block[{pos, toAdd}, pos = Flatten[Position[tree[[All, -1]], root]]; For[i = 1, i <= Length[pos], i++, toAdd = Flatten[Thread[{tree[[pos[[i]]]], {#}}]] & /@ nodes; (* check cycles!*) If[cycleQ[#] != True, AppendTo[tree, #]] & /@ toAdd; ]; tree = Delete[tree, {#} & /@ pos]; builtTree[#, matrix] & /@ Union[tree[[All, -1]]]; ]; ];
调用代码:initNode = 1; endNode = 6; lcycle = {}; tree = {{initNode}}; builtTree [initNode,matrix];
path:{{1}}根:1 – 节点:{2,3,4}
path:{{1,2},{1,3},{1,4}}根节点:2 —节点:{3,4,5}
path:{{1,3},{1,4},{1,2,3},{1,2,4},{1,2,5}}根:3 – 节点:{2, 4}
path:{{1,4},{1,2,4},{1,2,5},{1,3,4},{1,2,3,4},{1,3,2, 4},{1,3,2,5}}根:4 – 节点:{2,3,6}
path:{{1,2,5},{1,3,2,5},{1,4,6},{1,2,4,6},{1,3,4,6},{ 1,2,3,4,6},{1,3,2,4,6},{1,4,2,5},{1,3,4,2,5},{1,4, 3,2,5}} root:5 —节点:{6}
结果:{{1,4,6},{1,2,4,6},{1,2,5,6},{1,3,4,6},{1,2,3,4, 6},{1,3,2,4,6},{1,3,2,5,6},{1,4,2,5,6},{1,3,4,2,5,6},{ 6},{1,4,3,2,5,6}}
…不幸的是,我不能上传图像,以更好的方式显示结果:(
如果你想要所有的path,使用recursion。
使用邻接表,最好创build一个函数f(),试图填充当前访问的顶点列表。 像这样:
void allPaths(vector<int> previous, int current, int destination) { previous.push_back(current); if (current == destination) //output all elements of previous, and return for (int i = 0; i < neighbors[current].size(); i++) allPaths(previous, neighbors[current][i], destination); } int main() { //...input allPaths(vector<int>(), start, end); }
由于vector是按值传递的(因此在recursion过程中进一步下降的变化不是永久的),所有可能的组合都被列举出来。
你可以通过引用传递前一个向量来获得一点效率(因此不需要一遍又一遍地复制向量),但是你必须确保手动获得popped_back()。
还有一件事:如果graphics有周期,这将无法正常工作。 (我假设在这种情况下,你会想要find所有简单的path,然后)添加到前一个向量之前 ,首先检查它是否已经在那里。
如果您想要所有最短的path,请使用Konrad对此algorithm的build议。
你想要做的事情本质上是在(定向?)图中的两个顶点之间find一条path,如果需要最短path,请检查Dijkstraalgorithm ,或者如果需要任何path,请编写一个简单的recursion函数。