这个标准化数据的代码是如何工作的？

我有一个机器学习课程提供的standardizefunction没有很好的文档，我仍然是MATLAB新手，所以我只是试图分解function。 对标准化的语法或总体思路的任何解释都会有很大的帮助。 我们使用这个函数来标准化大matrix中提供的一组训练数据。 细分代码片段的大部分内容将对我有很大的帮助。 非常感谢。

 function [X, mean_X, std_X] = standardize(varargin) switch nargin case 1 mean_X = mean(varargin{1}); std_X = std(varargin{1}); X = varargin{1} - repmat(mean_X, [size(varargin{1}, 1) 1]); for i = 1:size(X, 2) X(:, i) = X(:, i) / std(X(:, i)); end case 3 mean_X = varargin{2}; std_X = varargin{3}; X = varargin{1} - repmat(mean_X, [size(varargin{1}, 1) 1]); for i = 1:size(X, 2) X(:, i) = X(:, i) / std_X(:, i); end end 

Answer 1

该代码接受大小为M x N的数据matrix，其中M是来自该matrix的一个数据样本的维度， N是样本的总数。 因此，这个matrix的一列是一个数据样本。 数据样本全部水平堆叠，并且是列。

现在，这个代码的真正目的是取出matrix的所有列并对数据进行标准化/标准化 ，以使每个数据样本performance出零均值和单位方差 。 这意味着在这个变换之后，如果你find了这个matrix中任何一列的平均值，它将是0，方差将是1.这是一个非常标准的方法来统计分析，机器学习和计算机视觉。

这实际上来自统计分析的z分数 。 具体来说，归一化方程式是：

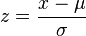
给定一组数据点，我们用这些数据点的平均值减去所讨论的值，然后除以相应的标准偏差。 你如何调用这个代码如下。 给定这个我们称之为Xmatrix，有两种方法可以调用这个代码：

• 方法＃1： [X, mean_X, std_X] = standardize(X);
• 方法＃2： [X, mean_X, std_X] = standardize(X, mu, sigma);

第一种方法自动推断X的每一列的平均值和X的每一列的标准偏差。 mean_X和std_X都将返回1 x N向量，给出matrixX中每列的均值和标准差。 第二种方法允许您为X每列手动指定平均值（ mu ）和标准差（ sigma ）。 这可能用于debugging，但是在这种情况下，您可以将mu和sigma指定为1 x N向量。 mean_X和std_X返回值与mu和sigma相同。

这个代码有点写得不好，恕我直言，因为你当然可以实现这个向量化，但代码的要点是，如果我们正在使用方法1，它findmatrixX的每一列的平均值，复制这个向量，所以它变成一个M x Nmatrix，然后我们用X减去这个matrix。 这将减去每个列各自的平均值。 我们也计算平均减法之前每列的标准偏差。

一旦我们这样做，然后我们通过将每列除以其相应的标准偏差来标准化我们的X 顺便说一句，做std_X(:, i)是多余的，因为std_X已经是一个1 x N向量。 std_X(:, i)表示抓取第i列的所有行。 如果我们已经有了一个1 x N向量，这可以简单地用std_X(i)来代替 – 对我来说有点矫枉过正。

方法＃2执行与方法＃1相同的事情，但是我们为X每一列提供了我们自己的平均值和标准差。

为了文档的缘故，我将如何评论这些代码：

 function [X, mean_X, std_X] = standardize(varargin) switch nargin %// Check how many input variables we have input into the function case 1 %// If only one variable - this is the input matrix mean_X = mean(varargin{1}); %// Find mean of each column std_X = std(varargin{1}); %// Find standard deviation of each column %// Take each column of X and subtract by its corresponding mean %// Take mean_X and duplicate M times vertically X = varargin{1} - repmat(mean_X, [size(varargin{1}, 1) 1]); %// Next, for each column, normalize by its respective standard deviation for i = 1:size(X, 2) X(:, i) = X(:, i) / std(X(:, i)); end case 3 %// If we provide three inputs mean_X = varargin{2}; %// Second input is a mean vector std_X = varargin{3}; %// Third input is a standard deviation vector %// Apply the code as seen in the first case X = varargin{1} - repmat(mean_X, [size(varargin{1}, 1) 1]); for i = 1:size(X, 2) X(:, i) = X(:, i) / std_X(:, i); end end 

---

如果我可以build议另一种方式来编写这段代码，我会使用威力强大的bsxfun函数。 这避免了必须做任何重复的元素，我们可以做到这一点。 我会重写这个函数，看起来像这样：

 function [X, mean_X, std_X] = standardize(varargin) switch nargin case 1 mean_X = mean(varargin{1}); %// Find mean of each column std_X = std(varargin{1}); %// Find std. dev. of each column X = bsxfun(@minus, varargin{1}, mean_X); %// Subtract each column by its respective mean X = bsxfun(@rdivide, X, std_X); %// Take each column and divide by its respective std dev. case 3 mean_X = varargin{2}; std_X = varargin{3}; %// Same code as above X = bsxfun(@minus, varargin{1}, mean_X); X = bsxfun(@rdivide, X, std_X); end 

我会争辩说，上面的新代码比使用和repmat快得多。 事实上，已知bsxfun比前一种方法更快 – 特别是对于较大的matrix。